問題1:単純立方格子において、次のミラー指数で与えられる面を図示せよ。 (110) (211) (422) (210) (111) 問題2:半径aの原子がFig 21のように層状に重なっている。面心立方格子(fcc)はABCABC・・・のように重 Qミラー指数:面間隔dを求める式について 隣接する2つの原子面の面間隔dは、ミラー指数hklと格子定数の関数である。立方晶の対称性をもつ結晶では Q面間隔の求め方 1)塩化ナトリウム結晶中におけるNaとClの原子間距離は02である。ミラー指数(0)、と4 結晶学的点群– その1 (3つの結晶学的軸を考慮した点群) 第1ポジション(主軸) 第2ポジション 第3ポジション 晶系 23、m3、432、 43m、m3m 立方 2、m、4、4 X 3、3 体対角 無、2、m 面対角
1
ミラー指数 面間隔 証明
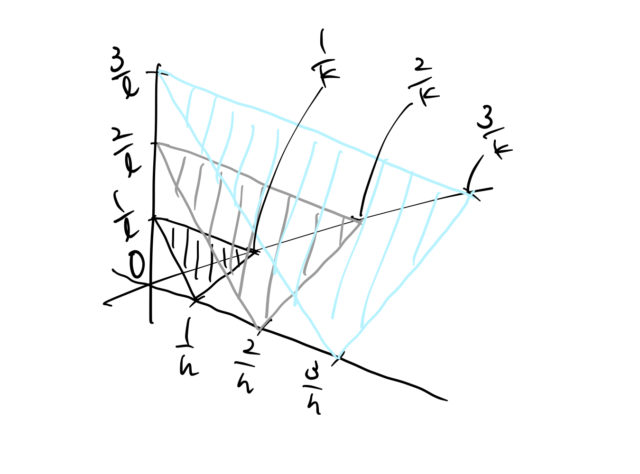
ミラー指数 面間隔 証明-逆格子の原点から, の座標の点に引いたベクトル は,ミラー指数 の格子面に垂直である. (1411) の長さは 面の面間隔の逆数に等しい. (1412) (証明) 面の中で原点に最も近い面の一部 原点から点a,b,cまでのベクトル(b)面の間隔 ミラー指数は,面と面の間隔を表すのに非常に役立つ.図・11に 示す正方格子における{hkl}面の間隔は次式で与えられる. 2 0 ()2 2 1 2 2 2 2 0 1 h k a, d a h k d hk hk = = 2 ()2 2 2 1 2 2 2 2 2 1 h k l a, d a h k l d hkl hkl = = 2 2 2 2 2 2 2 1 c l b k a h dhkl



結晶面の面間隔
6 ミラー指数その1:結晶における 方向の記述 7 ミラー指数その2:六方晶における ミラー指数 8 面間隔の求め方 9 格子欠陥(原子空孔と転位)・多結晶体 10 x線の発生法・特性x線について 11 ブラッグの条件と面の間隔 12 粉末x線回折による格子定数の求め方 隣接する2つの原子面の面間隔dは、ミラー指数hklと格子定数の関数である。立方晶の対称性をもつ結晶では d=a/√(h^2 k^2 l^2) ・・・(1) となる。 質問:「(1)式を証明せよ」と言われたのですが、どうす その他(教育・科学・学問) 解決済 教えて!goo原点に最も近い面 原点に近い面と の交点 a 3 原点に近い面と の交点 b b 2 この面を考える 軸との交点 17 2 33 a 軸との交点 b 17 3 22 OB b b 32, 77 hkcc 整数 7 を掛けて h = 3, k = 2 ミラー指数
り面とすべり方向の組み合わせを,すべり系(slip system)と呼ぶ. 図23 に,面心立方晶(FaceCentered Cubic),体心立方晶(BodyCentered Cubic)及び六方最密充 填(Hexagonal ClosePacked)の結晶構造を示す.また,表21 にそれらの結晶構造を持った金属材料の13 格子面と面間隔 c a b 3a 2b 2c 図3 ミラー指数 単位格子の外形や格子点の並びで構成される格子面あるい は、結晶の原子で構成される原子面を表す方法にミラー指数と 呼ばれるものがある。面の方程式に倣って切片を利用する方法 である。面の方程式はのa軸との切片は1なのでミラー指数は(100)と なる.(イ)oCの場合は第1面のa軸との切片は½ なのでミラー指数は(0)となる. 図4 (ア)oC格子を慣用(複合)単位胞で記述すると格 子面(グレー色)のミラ-指数はh+k=2nという
合わせh, k, l を面のミラー指数といい,この面に平行で等間隔な面の集合を (h k l) と表す.ただし六方晶では – (h k) = i とおいて,(h k i l) と表す 図15 いろいろな面のミラー指数 右の面はa, b, c 軸と1a, 2b, 3c で交わる.ミラー指数 (h k j l) をもつ格子面の面間隔を求めよ。 六方晶の格子ベクトルは 逆格子ベクトルは c a x y O A a A ミラー指数 (h k j l) をもつ格子面に対応する逆格子は で 面間隔は 応用実際の結晶では互いに平行で等間隔の距離で並んでいる結晶面が無数にならんでいるのです. このような1組の面の集合を結晶格子面といいます. 結晶ではこんな結晶格子面がたくさんあります. これを表したいときに使うのがミラー指数(Miller index)です.
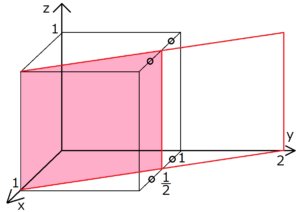



格子面とミラー指数の求め方




13 号 sicエピタキシャルウエハおよびそれを用いたsic半導体素子 Astamuse
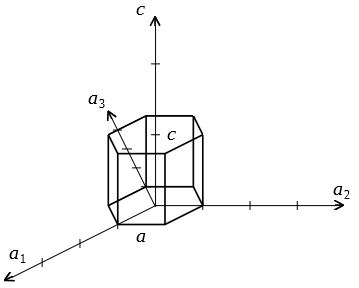
332六方格子のミラー指数 図312六方格子のミラー指数 立方格子との相違→a1,a2,a3,c の4軸を考える点 a1,a2,c 軸をα,β,δで横切る面 a/α :a/β :c/δの最小の整数比h:k:m を求める. 次に最後の指標をl=(hk) のように決める.19 結晶面の指数 三次元格子の面に対するミラー指数は(h k l)で 与えられる。 1) 格子定数 a 1, a 2, a 3 を単位として面が結晶軸 2 を切り取る長さを表す。 2) これらの数の逆数を求め、じ比を なす3個の最小の整数に簡約する。 これをその結晶面の面指数(h k l)と波長219ÅのX 線を照射した場合,ミラー指数 (111)の面に対応す る回折角 θ は 5717°であった.この立方晶の格子定数を求めよ.ただし, sin57l7°=084 とす る. (2)面心立方構造および体心立方構造の充填率をそれぞれ




物性物理学1 2 物質の構造 Yukishiomi Note



放課後化学講義室 X線回折のデータ解析をするプログラム
ち"にする(ガラス面と高さを一致させる)。 (2) 薄めたフィクサチフを用いて、試料を固める。スポイトを用い、縁の部分からしみ こませるようにする。5分程度で固まる。 32 装置の起動 (1) Mini Flex本体の背面にあるブレーカーおよび電源スイッチON。格子面間隔の計算 鈴木 実 逆格子の基本並進ベクトルをa ,b ,c ,格子面のミラー指数をh, k, lとする。(h;k;l)面の格子面間隔d は 2ˇ d = jKj (1) で与えられる.ただし, K= ha kb lc (2) である(「固体物性と電気伝導」(森北出版) p11).4 x線回折 1 目的 銅の粉末試料を用いたx 線回折測定を行い、粉末x 線回折の測定方法と測定原理について学ぶ。 また、得られたx 線回折のデータから格子定数の計算や結晶構造の同定を行えるようになる。 あ わせて、結晶を取り扱う上で重要な逆格子やミラー指数の概念についても理解する。
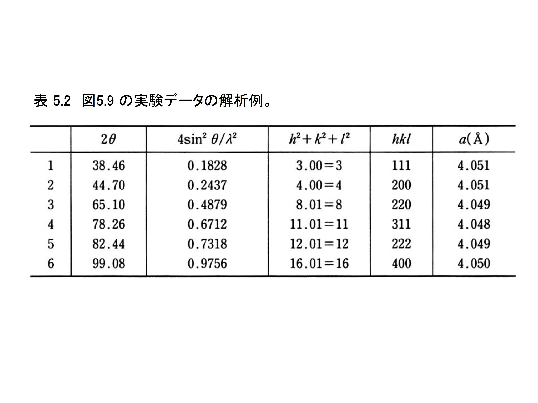



粉末x線回折による解析例



Information
) 面は直接格子の基本並進ベクトル a, a, a を 1 2 3 1/ h, 1/ k, 1/ l で切る平面のことである(ミラー指数のこと)。 (hkl)面とそれに垂直な逆格 子ベクトル K hkl 前ページの図に示すように、 逆格子ベクトル K hkl は(h k l) 面に垂直 であること意味している 六方晶の面を表す時にミラー指数でお馴染みの(hklm)についてどうもh k = iという関係が成り立つみたいです。ミラー指数については分かるのですが、何故この式が成り立つのかイマイチ腑に落ちない所があります。どなたか教えて頂けませ 面間隔 指数の隣り合った面間の距離は次の関係で求めることができる。ただし、格子定数を、単位格子の体積をとする。 立方晶: 正方晶: 斜方晶: 六方晶: 単斜晶: 三斜晶: 単位格子の体積 また、単位格子の体積は次の式で求められる。 立方晶: 正方晶: 斜方晶: 六方晶: 単斜晶:
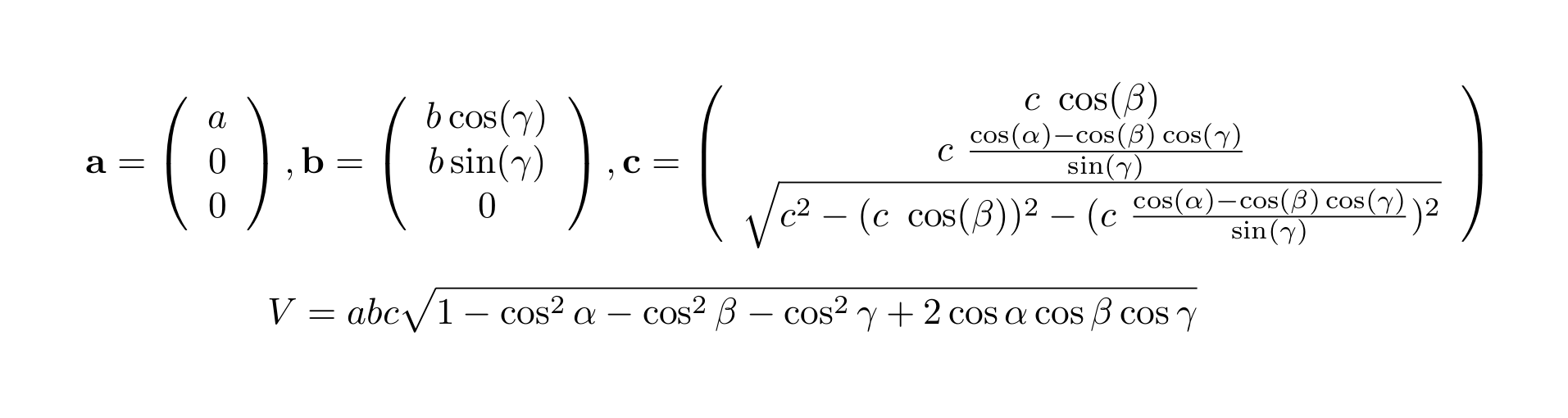



逆格子点の計算の理論背景 Theoretical Background For Calculation Of Reciprocal Lattice And Reciprocal Lattice Points To Cause Diffraction



ミラー指数と逆格子ベクトル 面間隔 幾何学的関係 ばたぱら
11 三斜 単斜 斜方 三方(菱面) 正方 六方 立方 なし 1本のc2 3本の直交c2 1本のc3 1本のc4 1本のc6 正四面体配置 の4本のc3 12 図・5立方晶系に属する単位胞には,正四面体的に配列した4本ミラー指数 ミラー指数の表記 立方晶における主要な面 立方晶における重要な関係 ( hkl)!hkl dhkl= a h2k2l2 a:格子定数 面間隔 6ますが,kfの 方向がこの面から外れて3次元的になるの が一般的ですkiを 固定して可能なkfの方向をすべて描 けば球となりますこ れが回折球とかLaue球 と呼ばれる ものです図1の ような2次元の図だと
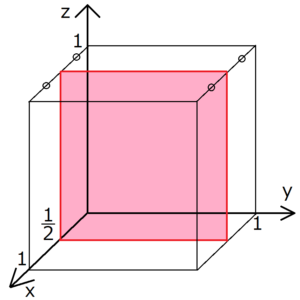



格子面とミラー指数の求め方



ミラー指数 面 物理のかぎしっぽ
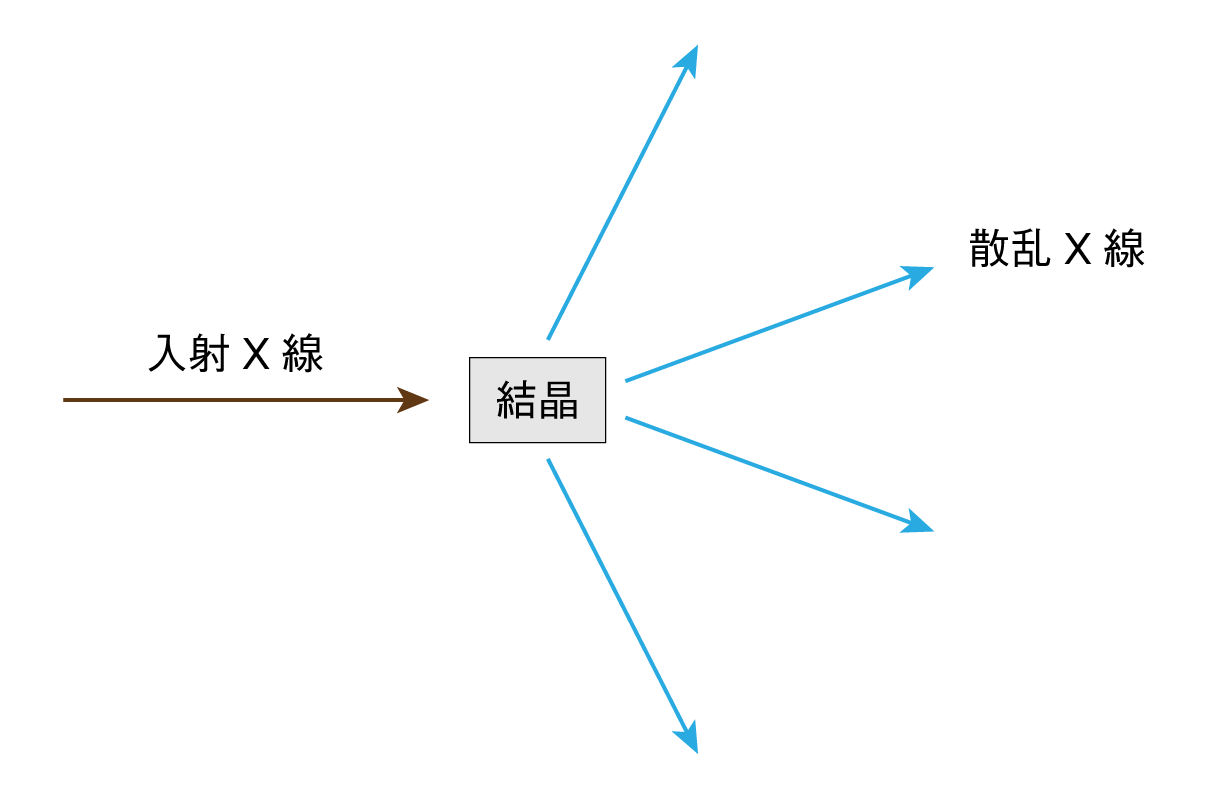
原子面の間隔によって生じる入射波と反射波の行路差 2asin n 2asin これが波長の整数倍であれば、各原子面からの散乱波の位相が等しい 等位相面 n:0,1,2,3,・・・証明 (1) ベクトル解析の相反基底の公式 3 (2) においては,ベクトルと相反基底との関係が,A ・a = 1 ですが,それをここでの定義,A ・a = 2π に変える必要があります。 (2) ( h k l ) 面(右下図の緑色の三角形を含む面)内の任意の異なる2点を示すベクトルは,代数・幾何学の公式から結晶面の指数 hkl方向とは・・・a 1 a 2 a 3 (hkl)面とは・・・a 1方向に1/h, a 2方向に1/k, a 3方向に1/l, で定義される3点を含む平面 h 1 k 1 l 1 r ha 1 ka 2 la 3 ベクトルrの方向 rに意味はない r hkl方向



ミラー指数 面 物理のかぎしっぽ
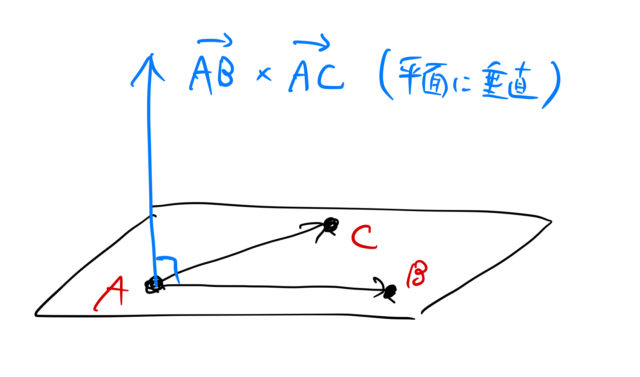



ミラー指数と逆格子ベクトル 面間隔 幾何学的関係 ばたぱら
は (h k l) 面の最小間隔 証明 (h k l) 面に垂直なベクトル 原点から (h k l) 面までの距離 d l 格子面と逆格子の関係 6 9 格子 逆格子 2次元格子の例 610 格子面 ミラー指数(23) 逆格子点(23) d G304 ミラー指数 fdenshicom 更新日: 結晶学で等価な原子や原子配列面を参照するために必要な用語のまとめです。面間隔 d 光路差}} 入射波 回折波 透過波 結晶面} } 波長 図54 ブラッグ条件の図解。 簡潔明瞭で、極めて実用的。 スカスカな結晶面が、鏡のように反射するしくみが、よくわからない。 結晶面の取り方が無数にあり、結晶面の正体が、はっきりしない。



ときわ台学 結晶構造 逆格子空間



2
れば全体として回折強度は現れません。格子面の数が奇数ならば余った格子面1枚分から の回折強度が残ることになりますが,全部の格子面からの反射が強め合う場合に比べれば 無視できる程度の強さでしょう。 一般的に, (l / m) λ = 2 d sin θ逆格子とミラー指数 8 単位格子のa,b,c軸と(h k l)面を考えると 逆格子ベクトルr* = ha* kb* lc*は(h k l)面と直交し、 (h k l)面の面間隔d (hkl)は1/r*に等しくなる ここで散乱ベクトルkを入射X線ベクトルk 0と 散乱X線ベクトルk 1で表し、その散乱角が2θだとしたら ミラー指数の決め方 とある格子面のミラー指数は、その格子面を無限に延長させたときのx,y,z軸の切片の逆数で表せる。下に具体例を挙げる。 例題 (1,0,0) 上の図の赤く塗られた格子面のミラー指数を考える。 まずx軸の切片は明らかにx=1である。



2



ミラー指数と逆格子ベクトル 面間隔 幾何学的関係 ばたぱら
(100)面の面間隔をd100 とすると、ja1j = d100 であり、hb1 a1 = q1 a1 = qa1 d100 の関係があ る。また、a1 方向の結晶の長さは、N1 d100 と表される。 従って、sin2 ˇqad100N1 = sin2 ˇqaL はqa = 1=Lのときに0となる。 x 0 05 1 15 2 100 80 40 60 N=10 sin2 (10 px) sin2 (px) h52 x 1/10 9/10 図7 Laue関数 さて、Bragg 条件はq = 2ksin でミラー指数:面間隔bを求める公式について 隣接する2つの原子面の面間隔dは、ミラー指数hklと格子定数の関数である。立方晶の対称性をもつ結晶では d=a/√(h^2 k^2 l^2) ・・・(1) となる。 ミラー指数は結晶格子の面や方位を表すために広く使われている表記法で、次のようなルールにしたがって表します。 ミラー指数 表している面または方位 軸を する点を結んで作られる面。 軸の負の方向に する点, 軸を する点を結んで作られる面。 は
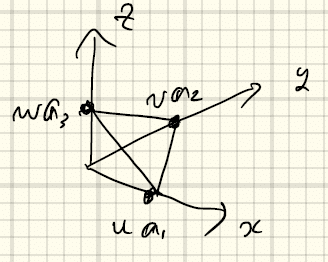



物性物理学1 2 物質の構造 Yukishiomi Note



格子面間隔の計算方法 六方晶 Sciencompass
心)や上下面の中心(底心),各面の中心(面 心)のように,元の単位格子の対称性を崩さな いように格子点を加えた格子.全部で14種類 存在する. 体心格子(bodycentered lattice) 底心格子(basecentered lattice) 面心格子(facecentered lattice) 13 d実空間格子の(hkl)格子面の間隔 λ光の波長 θ格子面と入射光のなす角 上の式の(hkl)は、格子面のミラー指数である。 ブラッグの反射条件は、結晶によるX線回折を考えるときに使結晶格子面の表し方 平行で等間隔な格子面の組 格子面が3軸を切る点をA, B, Cとし、原点Oからそれらの点に至る 距離をOA, OB, OCとする 格子点 u, v, w 整数 O A B C で与えられる h', k', l' は有理数であ



面のミラー指数を求める練習問題が解けず困っています 下の図のhとiのミ Yahoo 知恵袋




ミラー指数 Wikipedia



2



2



2




ミラー指数で表された面の図の書き方 化学徒の備忘録



のミラー指数 方向指数 の求め方が分かりません 教えて下さい Yahoo 知恵袋



x線結晶解析におけるラウエの条件式とブラッグの条件式



2
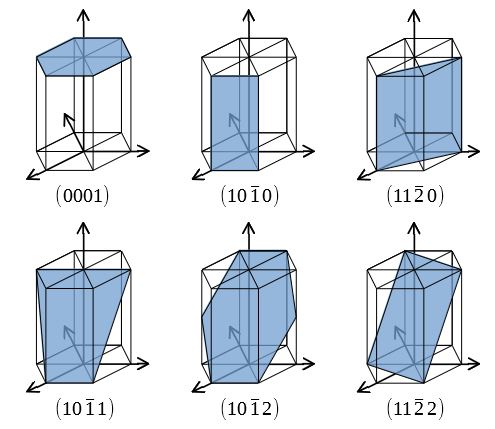



ミラー指数による立方晶 六方晶における面と方向の表し方



結晶面の面間隔
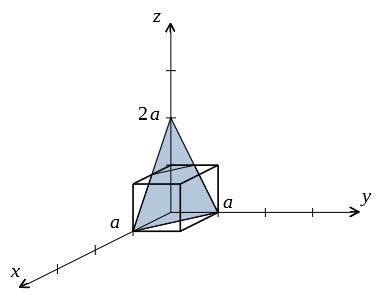



ミラー指数による立方晶 六方晶における面と方向の表し方



2




ミラー指数 面指数 ポップラーン



1
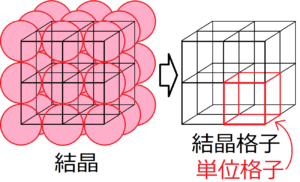



格子面とミラー指数の求め方
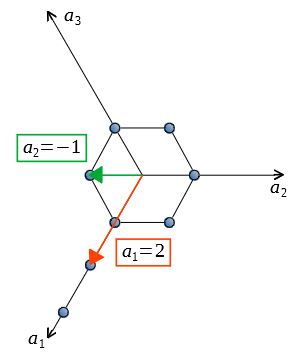



ミラー指数による立方晶 六方晶における面と方向の表し方



2




13 0631号 sicエピタキシャルウエハおよびそれを用いたsic半導体素子 Astamuse
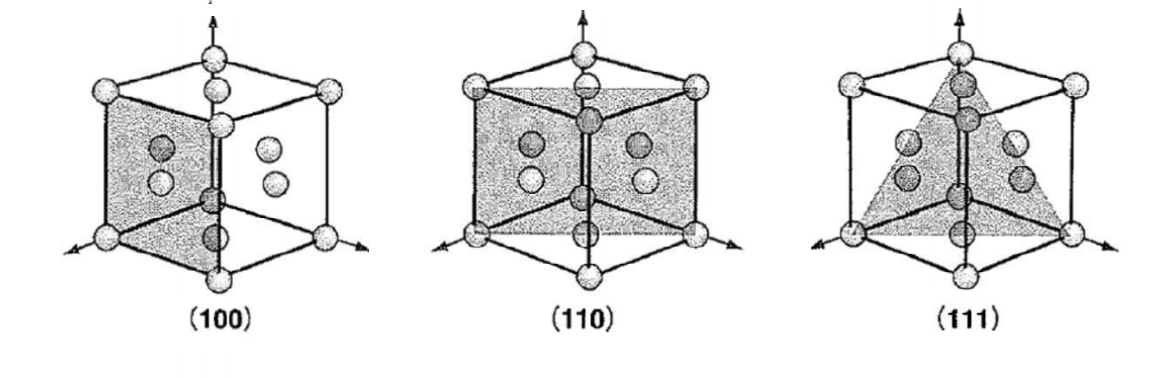



ミラー指数



2




ミラー指数で表された面の図の書き方 化学徒の備忘録



ミラー指数 面 物理のかぎしっぽ
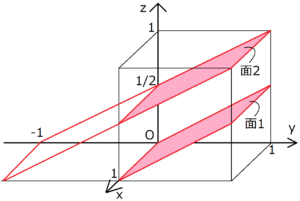



格子面とミラー指数の求め方
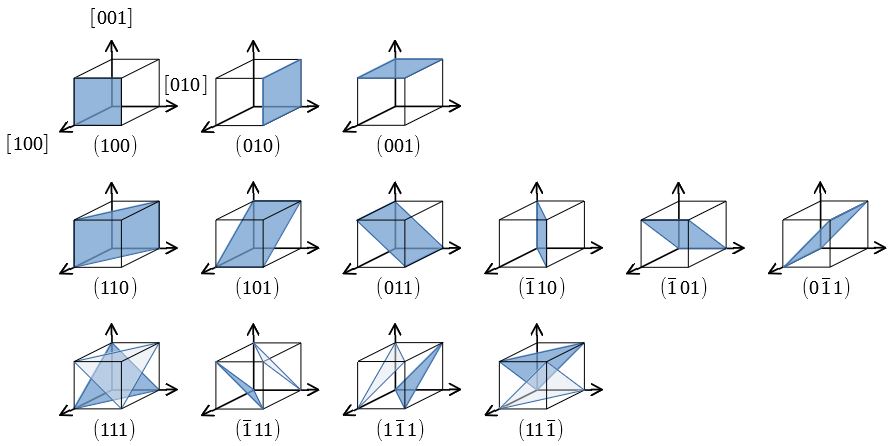



ミラー指数による立方晶 六方晶における面と方向の表し方




立方晶の面指数 ミラー指数 についてです 先日 テストに出た問題について Okwave



ミラー指数 面 物理のかぎしっぽ
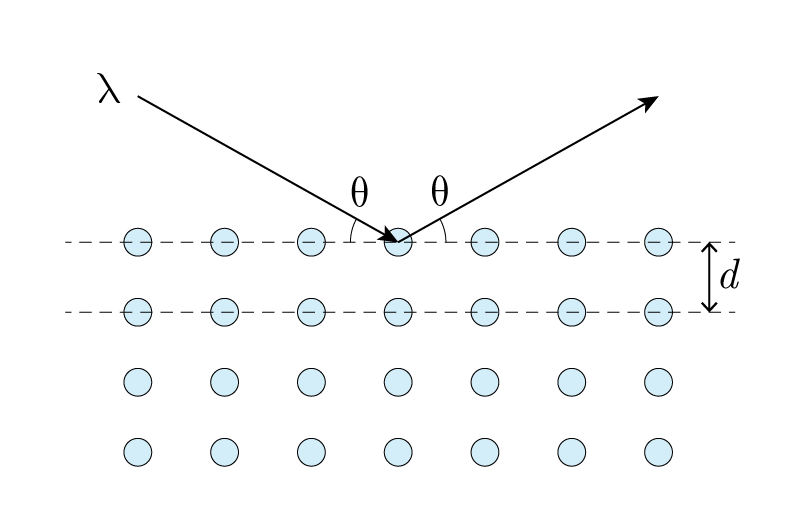



X線回折と平方数の話 物理学科 Advent Calendar Physics Lab 21



格子面間隔の計算方法 六方晶 Sciencompass



1



x線結晶解析におけるラウエの条件式とブラッグの条件式
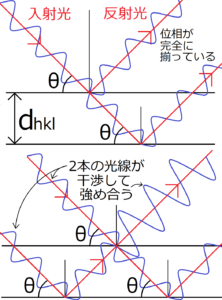



ブラッグの反射条件の導出とx線回折の原理について



結晶構造 ミラー指数 面指数 格子定数の求め方教えてください 求め Yahoo 知恵袋



2



2




ミラー指数で表された面の図の書き方 化学徒の備忘録



Chem Konan U Ac Jp



Information



2




逆格子 逆格子の基本ベクトルの定義と関係 化学徒の備忘録



格子面間隔の計算方法 立方晶 Sciencompass



Information



2



X線回折と平方数の話 物理学科 Advent Calendar Physics Lab 21




ミラー指数 面指数 ポップラーン



ミラー指数と逆格子ベクトル 面間隔 幾何学的関係 ばたぱら




ミラー指数で表された面の図の書き方 化学徒の備忘録



ミラー指数と逆格子ベクトル 面間隔 幾何学的関係 ばたぱら



ミラー指数 110 の図を真ん中に書いたのですが 面間隔とは左か右かどち Yahoo 知恵袋



x線結晶解析におけるラウエの条件式とブラッグの条件式




1 ミラー指数についてpart1 ゆっくり Youtube



ミラー指数による立方晶 六方晶における面と方向の表し方
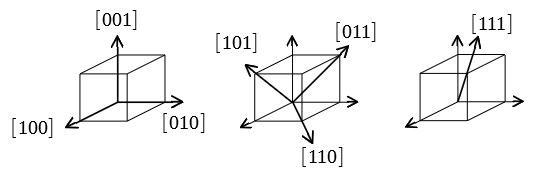



ミラー指数による立方晶 六方晶における面と方向の表し方



x線結晶解析におけるラウエの条件式とブラッグの条件式
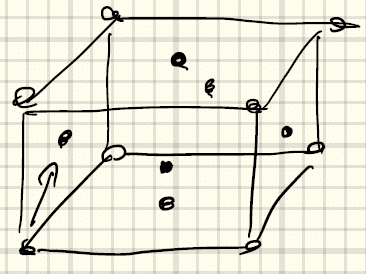



物性物理学1 2 物質の構造 Yukishiomi Note



1



ミラー指数 面 物理のかぎしっぽ




1 ミラー指数についてpart1 ゆっくり Youtube
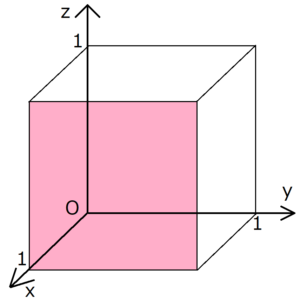



格子面とミラー指数の求め方




1 ミラー指数についてpart1 ゆっくり Youtube
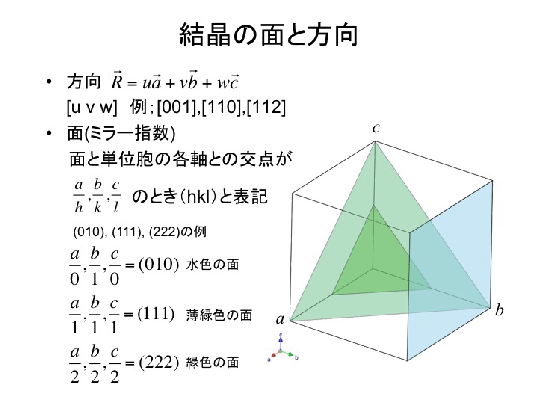



結晶の面と方向の記述方法




ミラー指数による立方晶 六方晶における面と方向の表し方
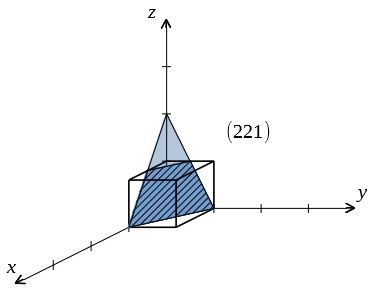



ミラー指数による立方晶 六方晶における面と方向の表し方
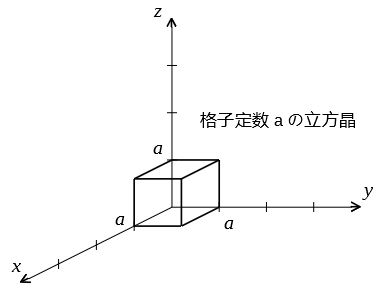



ミラー指数による立方晶 六方晶における面と方向の表し方




面間隔と単位格子の体積の計算式 化学徒の備忘録



シリコン格子定数の絶対測定とアボガドロ定数



ミラー指数の方向の問題です 何故このようになるのかさっぱりです 解き Yahoo 知恵袋



x線結晶解析におけるラウエの条件式とブラッグの条件式



2
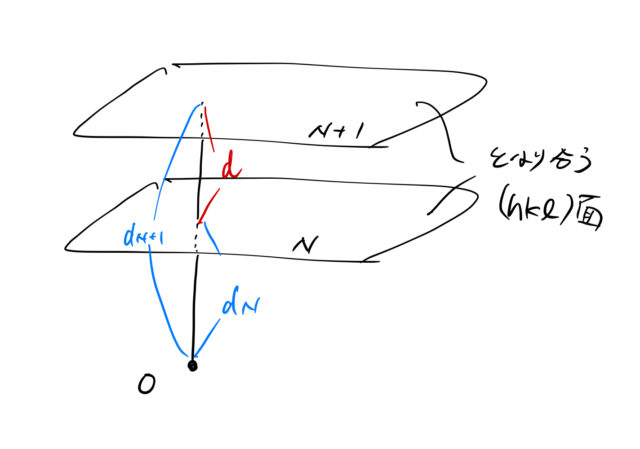



ミラー指数と逆格子ベクトル 面間隔 幾何学的関係 ばたぱら



2
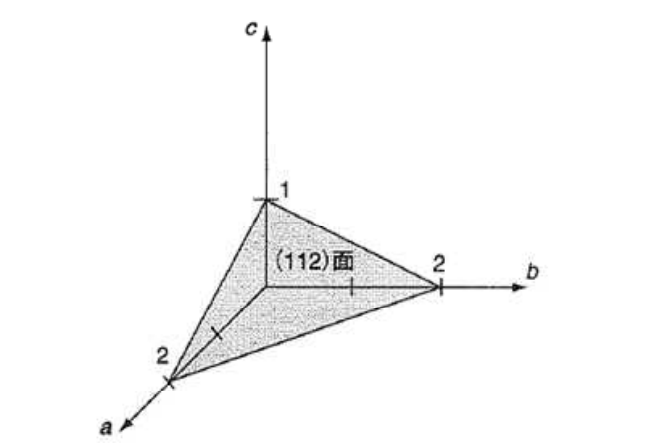



ミラー指数
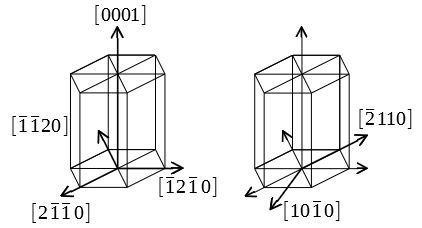



ミラー指数による立方晶 六方晶における面と方向の表し方
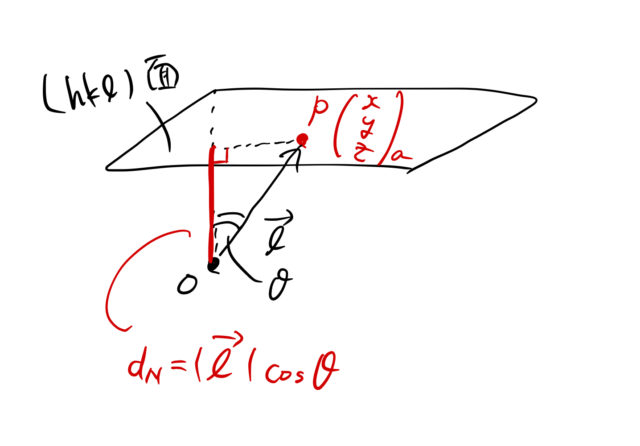



ミラー指数と逆格子ベクトル 面間隔 幾何学的関係 ばたぱら



結晶構造 ミラー指数 面指数 格子定数の求め方教えてください 求め Yahoo 知恵袋



ミラー指数が 101 のとき格子面が図のようになりました この Yahoo 知恵袋
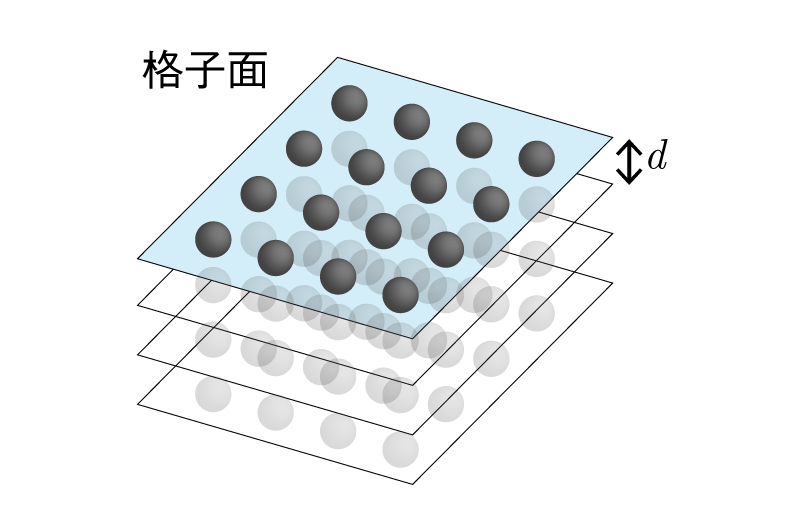



X線回折と平方数の話 物理学科 Advent Calendar Physics Lab 21



ミラー指数 110 の図を真ん中に書いたのですが 面間隔とは左か右かどち Yahoo 知恵袋
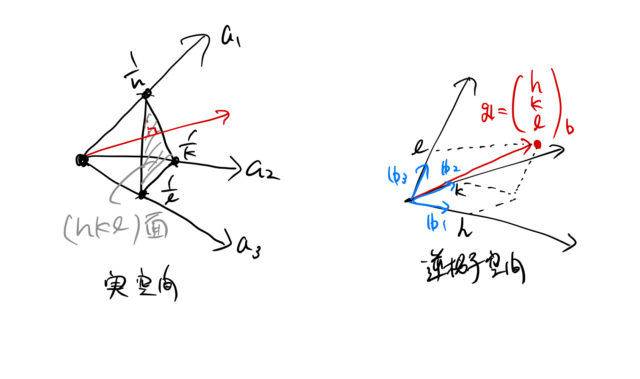



ミラー指数と逆格子ベクトル 面間隔 幾何学的関係 ばたぱら




ミラー指数 Wikipedia



2
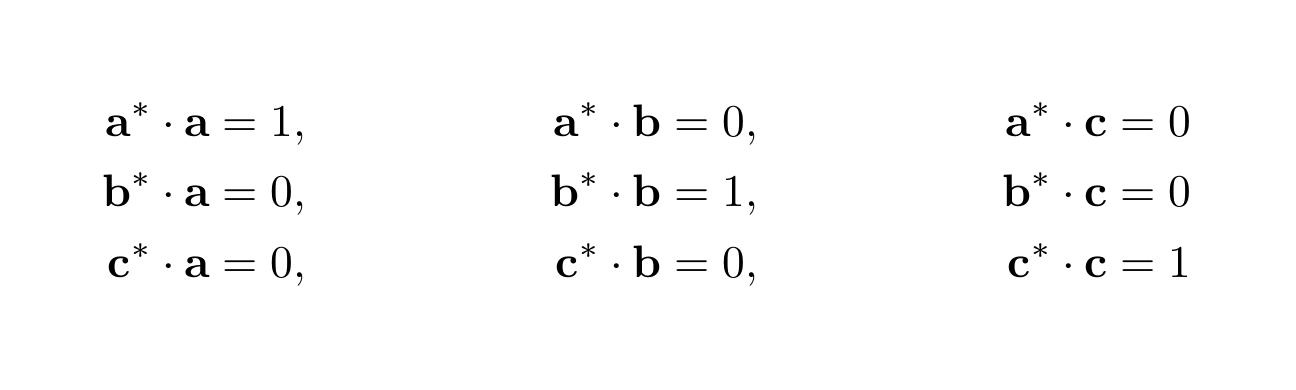



逆格子点の計算の理論背景 Theoretical Background For Calculation Of Reciprocal Lattice And Reciprocal Lattice Points To Cause Diffraction
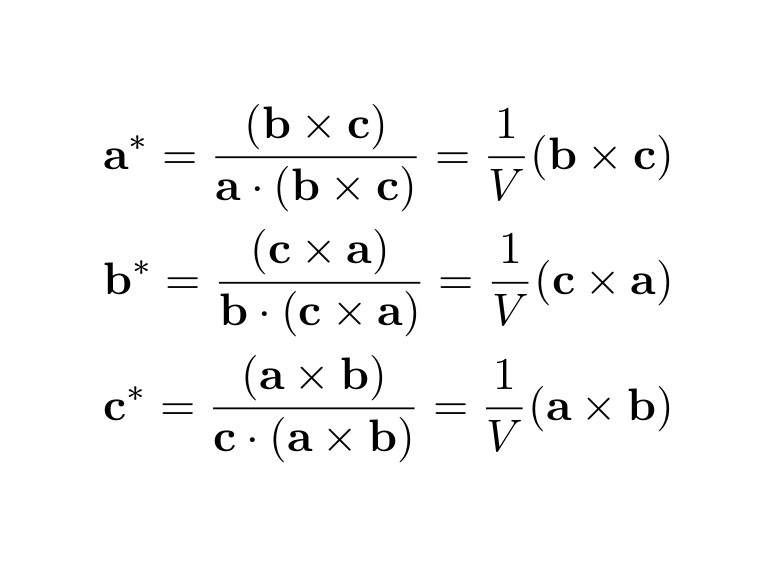



逆格子点の計算の理論背景 Theoretical Background For Calculation Of Reciprocal Lattice And Reciprocal Lattice Points To Cause Diffraction




04 号 x線回折による応力測定法 Astamuse



シリコン格子定数の絶対測定とアボガドロ定数



0 件のコメント:
コメントを投稿